MDS
Multidimensional scaling (MDS) projects items onto a plane fitted to given distances between points.
Inputs
- Data: input dataset
- Distances: distance matrix
- Data Subset: subset of instances
Outputs
- Selected Data: instances selected from the plot
- Data: dataset with MDS coordinates
Multidimensional scaling is a technique which finds a low-dimensional (in our case a two-dimensional) projection of points, where it tries to fit distances between points as well as possible. The perfect fit is typically impossible to obtain since the data is high-dimensional or the distances are not Euclidean.
In the input, the widget needs either a dataset or a matrix of distances. When visualizing distances between rows, you can also adjust the color of the points, change their shape, mark them, and output them upon selection.
The algorithm iteratively moves the points around in a kind of a simulation of a physical model: if two points are too close to each other (or too far away), there is a force pushing them apart (or together). The change of the point’s position at each time interval corresponds to the sum of forces acting on it.

- The widget redraws the projection during optimization. Optimization is run automatically in the beginning and later by pushing Start.
- Max iterations: The optimization stops either when the projection changes only minimally at the last iteration or when a maximum number of iterations has been reached.
- Initialization: PCA (Torgerson) positions the initial points along principal coordinate axes. Random sets the initial points to a random position and then readjusts them.
- Refresh: Set how often you want to refresh the visualization. It can be at Every iteration, Every 5/10/25/50 steps or never (None). Setting a lower refresh interval makes the animation more visually appealing, but can be slow if the number of points is high.
- Defines how the points are visualized. These options are available only when visualizing distances between rows (selected in the Distances widget).
- Color: Color of points by attribute (gray for continuous, colored for discrete).
- Shape: Shape of points by attribute (only for discrete).
- Size: Set the size of points (Same size or select an attribute) or let the size depend on the value of the continuous attribute the point represents (Stress).
- Label: Discrete attributes can serve as a label.
- Symbol size: Adjust the size of the dots.
- Symbol opacity: Adjust the transparency level of the dots.
- Show similar pairs: Adjust the strength of network lines.
- Jitter: Set jittering to prevent the dots from overlapping.
- Adjust the graph with Zoom/Select. The arrow enables you to select data instances. The magnifying glass enables zooming, which can be also done by scrolling in and out. The hand allows you to move the graph around. The rectangle readjusts the graph proportionally.
- Select the desired output:
- Original features only (input dataset)
- Coordinates only (MDS coordinates)
- Coordinates as features (input dataset + MDS coordinates as regular attributes)
- Coordinates as meta attributes (input dataset + MDS coordinates as meta attributes)
- Sending the instances can be automatic if Send selected automatically is ticked. Alternatively, click Send selected.
- Save Image allows you to save the created image either as .svg or .png file to your device.
- Produce a report.
The MDS graph performs many of the functions of the Visualizations widget. It is in many respects similar to the Scatter Plot widget, so we recommend reading that widget's description as well.
Preprocessing
When given Distances on the input, preprocessing is not applied. When given Data, MDS uses default preprocessing if necessary. Preprocessing is executed in the following order:
- continuizes categorical variables (with one feature per value)
- imputes missing values with mean values
To override default preprocessing, preprocess the data beforehand with Preprocess widget.
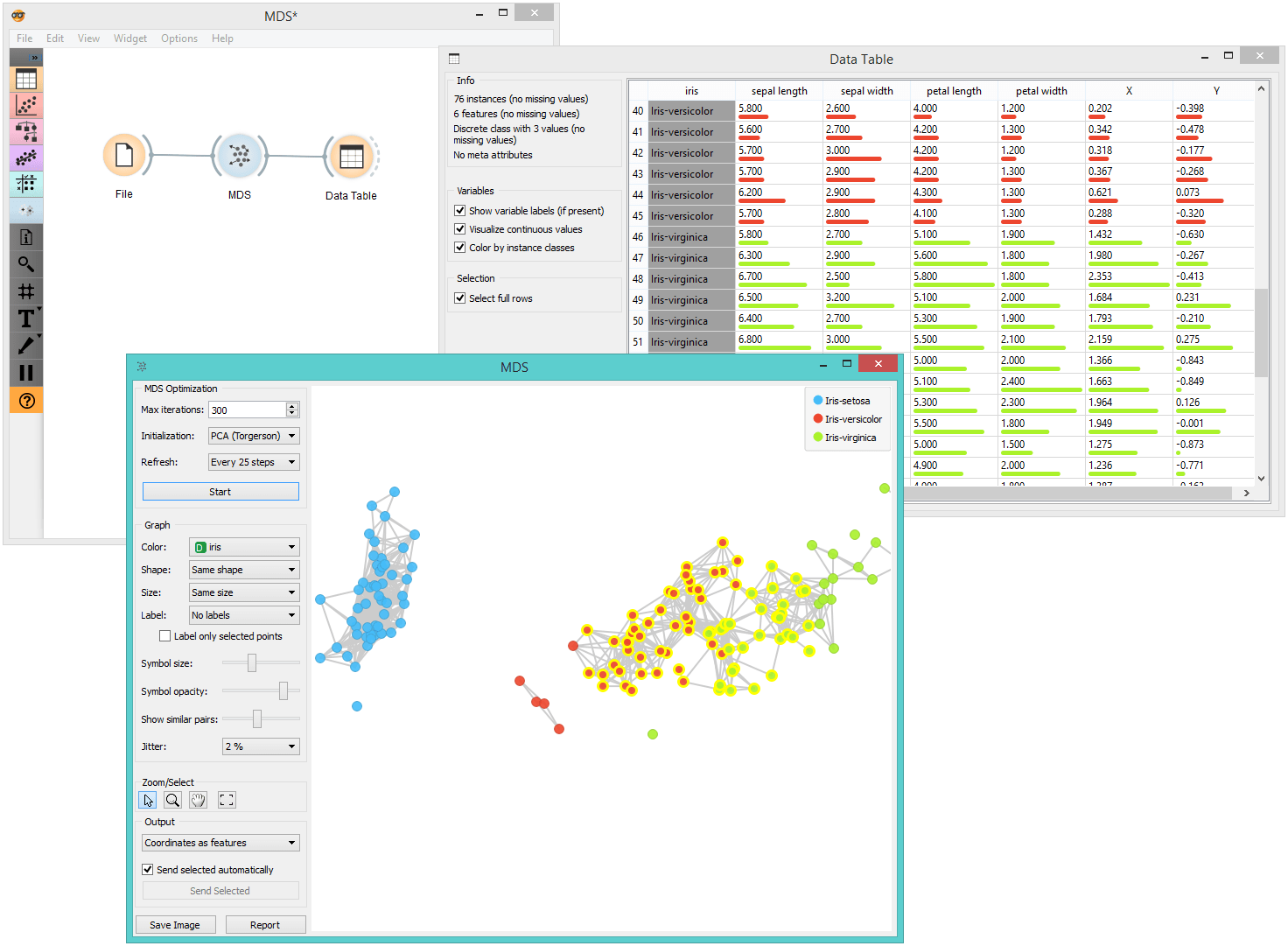
Example
The above graphs were drawn using the following simple schema. We used the iris.tab dataset. Using the Distances widget we input the distance matrix into the MDS widget, where we see the Iris data displayed in a 2-dimensional plane. We can see the appended coordinates in the Data Table widget.
References
Wickelmaier, F. (2003). An Introduction to MDS. Sound Quality Research Unit, Aalborg University. Available here.